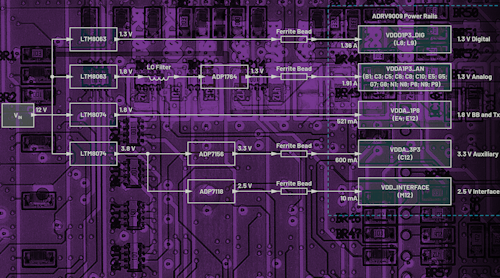
> >网站资源
..> >图书馆:TechXchange
. . . .>>科技交流:无线电设计101
|
|
下载。pdf格式的本文 该文件类型包括高分辨率的图形和原理图。 |
Delta-sigma模数转换器(adc)在支持中低速度和高分辨率应用方面的能力是令人着迷的——几乎是神秘的。它们利用了模拟电路的速度和数字电路的健壮性。它们还减少了转换器中使用的模拟电路的数量。更重要的是,电路的模拟部分不需要非常精确。当然,数字块必须工作在更高的采样时钟,因此,消耗更多的能量。
表的内容
一个delta-sigma ADC通常包括一个delta-sigma调制器,后跟一个抽取滤波器。Delta-sigma调制是数据转换器世界中最有效的转换形式之一。它的应用包括通信系统,专业音频和精密测量。
delta-sigma调制的目的是通过只传输连续样本之间值的变化(delta),而不是实际样本本身来实现更高的传输效率。adc和数模转换器(dac)都可以使用δ -sigma调制。
过采样在感兴趣的信号带宽内减少了噪声的影响,有利于δ -sigma ADC的模拟操作。接下来,噪声整形将噪声推到信号带宽之外。数字运算过滤掉了感兴趣范围之外的噪声。最后,这个数字滤波器对数据进行抽取或下采样。不过,在考虑调制器本身之前,有必要熟悉一些在转换器中扮演重要角色的概念:量化噪声、过采样和噪声整形。
在ADC中,量化信号可以描述为输入信号加上量化噪声:
V量化= V在+ε(1)
V量化和V在分别为量化信号和输入信号;ε是与此过程相关的误差,或量化器的输入和输出之间的差异。
转换器的全量程除以它的量化电平数定义了它的最低有效位(LSB)。n位转换器有2个N水平的量化。因此,任何这些量化级别的宽度都是FS/(2N- 1).对于量化宽度为∆的ADC,量化噪声在-∆/2和+∆/2之间的任何位置的概率相等,并且在量化误差范围内具有均匀的概率密度函数。量化噪声功率可以通过积分这个范围内的误差来计算,如下所示:
它描述了LSB宽度的噪声功率。但是,它可以被重写来表示比特数和满刻度:
一般来说,可以用比奈奎斯特频率大得多的频率对信号进行采样。采样频率(fs)与奈奎斯特频率(2fO)称为过采样比(OSR),其中fO为输入信号的频率。因此,OSR可以写成:
在过采样条件下,在信号带宽(0到f)内的噪声功率O)由:
如公式所示,过采样将带内均方根噪声降低到过采样比的平方根(图1)。
减少量化在:
|
|
下载。pdf格式的本文 该文件类型包括高分辨率的图形和原理图。 |
虽然对变换器的输入进行过采样可以降低噪声,但对于δ -sigma调制器来说,这种降低甚至更大。事实上,高阶调制器可以进一步降低噪声。1计算L阶、OSR为M阶调制器噪声的一般公式为:
注意,方程6可以由方程7得到,在没有使用delta-sigma调制的情况下。在这种情况下,调制的阶数被认为是零。
通过过采样,噪声频谱分布在更宽的频率范围内。sigma-delta的下一步是塑造噪声,将大部分噪声频谱推到更高的频率,从而显著降低带内噪声。这个概念被称为噪声整形(图2)。
这个简单的反馈系统可以表示为:
注意,在公式9中,当频率趋于0时,Y趋于输入分量x。随着频率的增加,第一项(包含输入信号分量)趋于0,输出趋于Q(n)。换句话说,在高频下,输出主要由量化噪声组成。总的来说,似乎一个低通滤波器在正向路径上作用于信号,而一个高通滤波器在反馈路径上作用于噪声。噪声整形已经实现!在那之后,所有需要做的就是过滤掉高频的噪声(图3)。
一阶delta-sigma调制器包括积分器、用作子adc的比较器和子dac(图4)。子dac可以像一个在两个参考电压之间切换的多路复用器一样简单。闩锁操作通常嵌入比较器中。
过采样可以提高信噪比。当噪声功率降低时,预期信噪比会增加。从定量的角度出发,从式2得到的非过采样变流器的量化噪声出发,量化噪声的理论信噪比用输入信号与噪声信号的比值表示:
其中N是转换器的比特数。式6表示过采样转换器的噪声功率。根据公式6和10,对于过采样比为OSR的转换器,其信噪比可计算为:
每增加一倍的采样频率,信噪比就提高3 dB或0.5 bit。例如,一个16位转换器的理论信噪比约为98 dB。但当过采样比为8时,信噪比增加3 dB/octave,即增加9 dB,信噪比增加到107 dB。
使用高阶模,delta-sigma将进一步提高信噪比。二阶调制器每增加一倍的过采样比,信噪比就提高15 dB。每一倍的过采样率所取得的改进一般可以由以下计算得到:
3(2L + 1)dB (13)
每增加一倍OSR。公式13还表明,对于一阶调制器(L = 1),每过采样比为2,就有9 db的改善。对于具有相同OSR的二阶调制器(L = 2),这种改进增加到15 db——也就是说,每增加一阶调制器,就有6 db的改进。
由于调制器的输出是一个数字比特流,因此很难在其输出处对数字化输入信号进行可视化和正确性检查(图5和表)。
例如,代码10111011是通过读取比较器每次比较的输出来获得的。本例中的完整刻度是(2.5 - (- 2.5))= 5 V。
在5v刻度上,因为较低的参考点位于-2.5 V,一个1v的信号将高于较低的参考点3.5 V。这是全量表的0.7(3.5/5 = 0.7)。产生的代码(HLHHHLHH或10111011)有6个高点和2个低点,所以8个比特流代码中有6个是高点。因此,平均值是6/8 = 0.75。这个平均值接近于输入的实际值(0.7)。
如果继续操作并获得更多的位,则平均值将越来越接近0.7。对于这种类型的调制器,可以理解为对于更接近+V的值裁判,调制器产生更多的高点。对于更接近于-V的输入值裁判,调制器产生更多的低点。一个典型的正弦波输入产生的代码在其两个峰值处有更多的高点或低点。当输入接近中间值时,平均而言,产生的1和0的数量变得可以比较(图6).
通常,调制器的阶数大于1(图7)。
由六阶调制器模型输出的比特流之后是一个抽取滤波器,形成一个24位的delta-sigma ADC,从而产生这个输出。同样,当输入振幅增加时,调制器产生更多的1,并向输入的最低电压移动,产生更多的0(图8).
1.Delta-Sigma数据转换器;理论,设计和模拟, S.R. Norseworthy, r.s reier, G.C. Temes, Wiley Interscience, 1997。
2.”Sigma-Delta调制器作为A/D转换器,“R.J. Van de Plassche,IEEE电路与系统汇刊,第25卷,1978年7月,第510-514页。
3.”过采样A/D转换原理,“马克斯·w·豪泽,音频工程学会期刊,第39卷第1/2号,1991年1月/2月,第3-26页
4.“多标准无线收发器抽取滤波器的设计与实现”,a . Ghaze等,IEEE无线通信汇刊2002年10月2日第1卷第4期。
5.”理解级联积分器梳状滤波器理查德•里昂。”嵌入式系统编程, 2005年3月,www.design-reuse.com/articles/10028/understanding-cascaded-integrator-comb-filters.html
6.”一种用于抽取和插值的经济类数字滤波器“E.B. Hogenauer,IEEE声学、语音和信号处理汇刊,第29卷第2期,1981年4月,第155-162页
7.”设计线性相位FIR抽取滤波器和∑-∂调节器,”A. Blad, P. Lowenborg, H. Johansson,第14届欧洲信号处理会议,2006
8.”低功耗抽取滤波器体系结构∑-∂adc,“Özge Gürsoy, Orkun Sağlamdemir, Mustafa Aktan, Selçuk Talay, Günhan Dündar
9.有关数据转换器的更多信息,请访问www.ti.com/dataconverters-ca.
该文件类型包括高分辨率的图形和原理图。