What you'll learn:
- Rectangular or cylindrical? Comparing the enclosure types.
- 确定壁厚。
- 外壳的方向如何影响性能?
InPart 1, we covered modal analysis, the Timoshenko differential equation of vibration, and the type of material to use for a design. Here, we’ll cover whether to use a rectangular or cylindrical enclosure, maximum recommended height, the effect of wall thickness, and the impact of orientation on performance.
Should I Design a Rectangular or a Cylindrical Enclosure?
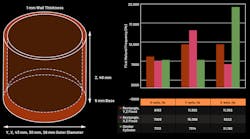
图1shows both a hollow rectangular and cylindrical stainless-steel extrusion, with 2-mm wall thickness and 40-mm height. The outer diameter of the cylinder is 43 mm, and the rectangular piece is also 43 mm on both x and y axes.
For modal analysis, the entire 2-mm wall surface (or x, y cross-sectional area) is a fixed constraint.图2显示模态有限元法(FEM)分析results. The first natural frequency with significant mean power frequency, or MPF (greater than 0.1 for the ratio of effective mass to total mass of the system), is plotted vs. material shape. The cylindrical shape has the highest first significant natural frequency for x and y axes, with similar performance in the z direction.
Geometry: Area and Inertia
等式1包括材料和几何依赖性。由于使用不锈钢参数模拟了矩形和圆柱形片,因此圆柱形片的性能更好的唯一原因是几何形状。
数字3illustrates the cylinder and rectangle cross-section for calculation of the area moment of inertia and cross-sectional area of the pieces.
The area moment of inertia (IYY) of the rectangle is almost 50% greater than that of the cylinder(Table 1)。矩形在承受变形方面更好。但是,圆柱体的横截面(A)比矩形大3倍。较大的A参数表示模拟和现实中较大的固定限制 - 圆柱体的设计更好地用于增加刚度或更高的刚度。
使用Table1values and Equation 2, the critical frequency is 60.74 kHz for the cylinder and 26.56 kHz for the rectangle. Equation 2 is a useful tool to show the relative performance of different geometries. Equations 1 and 2 predict four independent solutions below the critical frequency.
Table 2summarizes the FEM results and confirms the first four significant modes.
我的传感器推荐高度是多少?
公式1和2很有用,但是它们没有提供有关围栏垂直高度与可能的第一个重要固有频率之间的权衡的分析指导。从公式3中,我们可以直观地看到传感器围墙越高,第一个固有频率就越低。
Limitations of Analytical Models
Equations 1 and 2 assume that the width of a beam cross-section is at least 15% of the beam length.5Other approaches for long, thin beams, such as Bernoulli’s equation,6假设光束横截面的宽度小于光束长度的1%。5
For long, thin beams, Equation 46can be used, which includes length (L) or sensor height. Equation 4 doesn’t consider shear forces, which are important for short, thick beams. For first significant natural frequencies, there’s generally good agreement between equations 1,2, and 4 for solid cylindrical shapes. For hollow shapes, Equation 4 underestimates the first significant natural frequency by 50%.
Equation 46parameters include Young’s modulus (E) of stiffness, diameter (d), length (or height), density of material used (ρ), and Knconstants for given configurations.
As analytical models fail to provide guidance for height constraints for hollow enclosures, height studies typically rely on FEMs.
身高研究
为了提高外壳高度的性能降解指导,显示了图4were simulated.
The stainless-steel extrusions include a 5-mm base, which can be used to provide a stud screw mount between the enclosure and monitored equipment (for example, a motor). Increasing the height of the cylinder from 40 mm to 100 mm results in a reduced first significant natural frequency of 12.5 kHz to 3.3 kHz for x- and y-axes(Fig. 5)。Z轴也从31.2 kHz减少到12.7 kHz。对于高性能传感器,很明显必须将外壳高度最小化。
What is the Effect of Reducing Enclosure Wall Thickness or Diameter?
减少外壳壁厚
Table4shows the geometric and material properties when the cylinder in数字1is reduced from a 2- to a 1-mm wall thickness, but keeps the 40-mm height and 43-mm outer diameter.
使用Table4值和方程式2,对于2毫米的壁厚缸而言,临界频率为60.74 kHz,1毫米壁厚缸的临界频率为61.48 kHz。我两个YYand A parameters decreasing by about 50%, the numerator and denominator in Equation 2 are equally affected for the 1-mm wall-thickness cylinder. From this calculation, it’s assumed that both cylinders will perform similarly in FEM modal analysis.
In图6, the FEM results of first natural frequency with significant MPF (greater than 0.1 for the ratio of effective mass to total mass of the system) is plotted vs. cylinder wall thickness. The effect of reducing the cylinder wall thickness compared to natural frequency is very small.
Reducing Enclosure Diameter
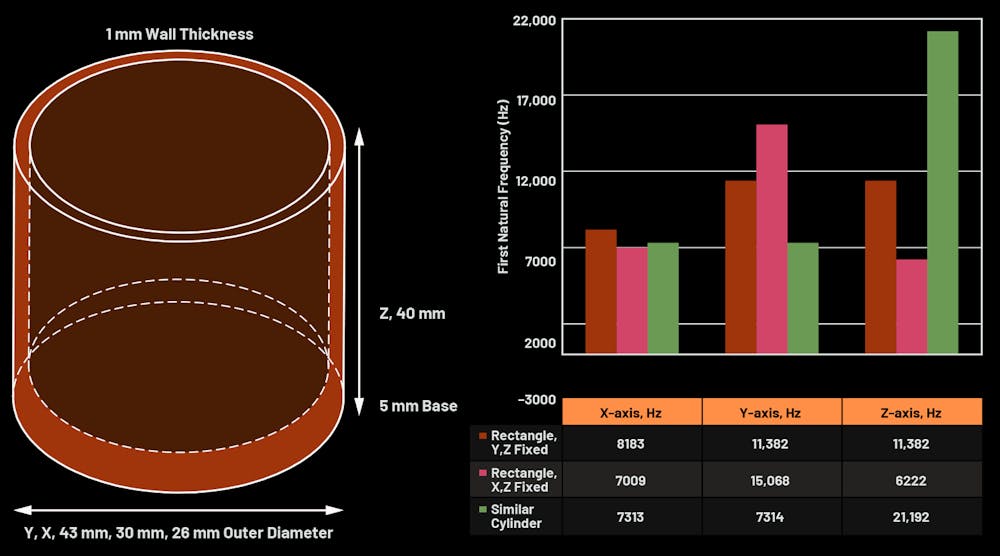
The examples presented so far have all focused on cylindrical enclosures with a 43-mm outer diameter. Some designs may only require 30- or 26-mm outer diameters.图7说明了仿真模型,并且图8显示了改变围墙外径的效果。
当减少汽缸从43毫米直径26 mm, the x- and y-axes’ first natural frequencies reduce by about 1.5 kHz, while the z-axis first natural frequency increases by 1.9 kHz. In changing the cylinder diameter, both the area moment of inertia (IYY) and the cross-sectional area (A) decrease. The IYY参数将比A参数降低更多。
In reducing the diameter from 43 mm to 30 mm, the IYY将减少2/3,而A将减少1/3。同样,引用方程式2,净效应是第一固有频率的逐渐下降。
Intuitively, reducing the cylinder diameter will make the structure less rigid, so it makes sense that the natural frequency will reduce. However, using simulation, it’s clear that the reduction in first natural frequency isn’t dramatic, and changing diameters can still result in a first natural frequency in the tens of kilohertz.
改变传感器围墙的方向会提高性能吗?
本文的先前部分表明,增加围墙的高度将导致第一固有频率降低。还显示的是,建议使用圆柱形外壳形状,而不是使用矩形形状。但是,在某些情况下,矩形形状很有用。
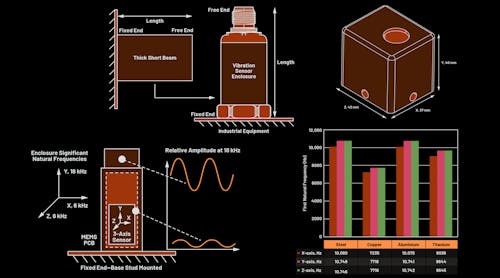
Consider a scenario where the enclosure needs to accommodate a sensor and circuit, with a defined 60-mm height and 43- × 37-mm breadth and width. Using a rectangular shape and changing the orientation of fixed constraint (equipment attachment) can help boost performance.
The rectangular enclosure shown in图9有多个附件孔;因此,围栏可以安装到各种方向上的设备上。如果外壳安装在x,z脸上,则外壳的有效高度为60 mm。但是,如果围栏安装在y,z面上,则有效高度仅为37毫米。这种方法可用于矩形外壳,但是使用圆柱体的弯曲表面不可行。
图10表明,通过更改外壳方向,可以提高X轴第一共振频率,并且与圆柱体相比,Y轴更好。与x,z固定方向相比,y,z固定方向的z轴第一共振频率较高,而频率模式几乎是两倍。但是,对于Z轴固有频率而言,圆柱体表现最好。与圆柱形相比,矩形形状是在三个轴上具有相似性能的良好方法。
在第3部分中,我们将使用单轴和三轴传感器,设计和模态分析,外部电缆仿真以及振动传感器安装涵盖设计。
Richard Anslow is a system applications engineer with the Connected Motion and Robotics Team within the Automation and Energy Business Unit at Analog Devices. His areas of expertise are condition-based monitoring and industrial communication design. He received his B.Eng. and M.Eng. degrees from the University of Limerick, Limerick, Ireland.
References
1。ANSYS创新培训班:Modal分析。ANSYS, 2021.
2. Stephen Timoshenko.Vibration Problems in Engineering, 4th edition. John Wiley and Sons Inc., New York, 1974.
3。Leszek Majkut. “Free and Forced Vibrations of Timoshenko Beams Described by Single Difference Equation.”Journal of Theoretical and Applied Mechanics, Vol. 47, No. 1, January 2009.
4。Mohammad Hossein Abolbashari, Somayeh Soheili, and Anoshirvan Farshidianfar. “Flexural Vibration of Propeller Shafts Using Distributed Lumped Modeling Technique.” The 16th International Congress on Sound and Vibration, Krakow, 2009.
5。Saida Hamioud and Salah Khalfallah. “Spectral Element Analysis of Free - Vibration of Timoshenko Beam.”International Journal of Engineering, 2018.
6. Olivier A. Bauchau和James I. Craig。Structural分析:WithApplications至Aerospace结构,施普林格,2009年。
7.TN17:InstallationofVibration传感器, Wilcoxon Sensing Technologies, 2018.
8. A. Khayer Dastjerdi, E. Tan, and F. Barthelat. “Direct Measurement of theCohesive Law of Adhesives Using a Rigid Double Cantilever BeamTechnique。”实验力学协会,2013年5月。